There are no items in your cart
Add More
Add More
| Item Details | Price | ||
|---|---|---|---|
Mastering the trade-offs for better machine learning models
Definition: Bias represents the error introduced by approximating a real-world problem, which may be complex, by a too-simple model. High bias means the model makes strong assumptions about the data, potentially missing important patterns.
Definition: Variance refers to the amount by which the model's learned function would change if it were trained on a different training dataset. High variance means the model is highly sensitive to the specific training data it saw.
Definition: Noise is the irreducible error in the data itself. It stems from inherent randomness, measurement errors, or unmodeled factors influencing the target variable.
Definition: An underfit model is too simplistic. It fails to capture the underlying structure of the data, performing poorly on both the training data and unseen test data.
Definition: An overfit model is too complex. It learns the training data extremely well, including noise and random fluctuations, but fails to generalize to new, unseen data.
Definition: This is the goal! An appropriately fit model captures the true underlying pattern in the data without fitting the noise. It performs well on both training and unseen test data.
The following diagram illustrates how different model complexities affect fitting the data. We want a model that captures the underlying trend without fitting the noise (Good Fit).
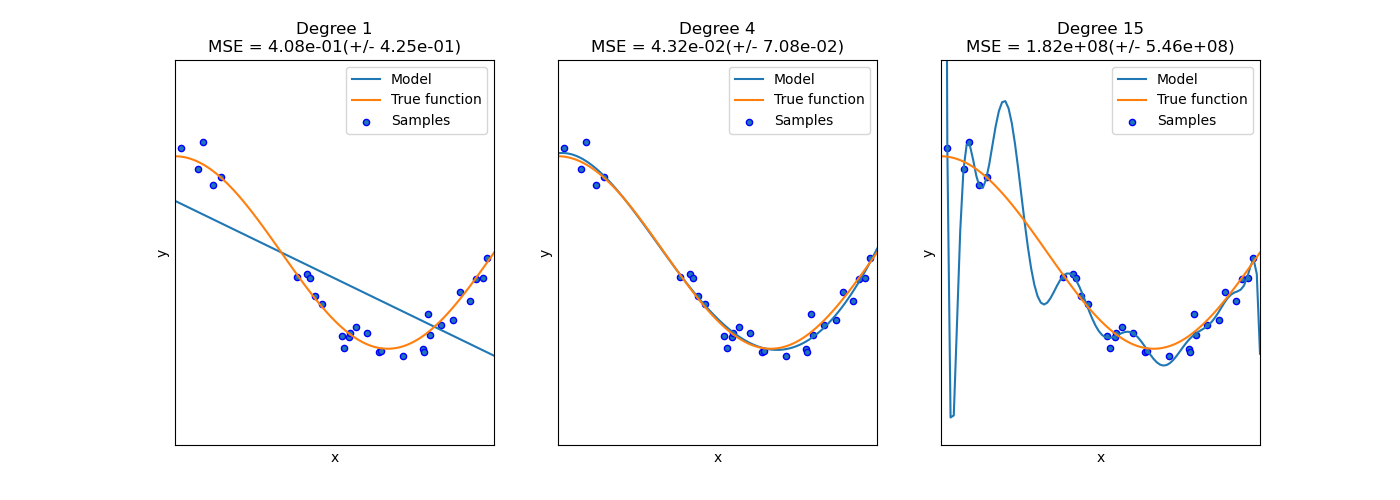
Image adapted from: Scikit-learn Documentation
As shown:
This illustrates the trade-off: increasing model complexity generally decreases bias but increases variance. The sweet spot is finding the complexity that minimizes the *total* error on unseen data.
When your model suffers from high variance (overfitting), consider these strategies:
| Problem / Scenario | Diagnosis & Solution | Key Takeaway |
|---|---|---|
| A linear regression model shows high error (e.g., RMSE) on both the training set and the test set. | The model is likely underfitting (high bias). Try a more complex model (e.g., polynomial regression, add interaction features) or engineer better features. | High train/test error suggests underfitting (high bias). |
| A deep neural network achieves 99% accuracy on the training set but only 75% accuracy on the test set. | The model is likely overfitting (high variance). Try adding dropout, L2 regularization, getting more data, or reducing network size (fewer layers/neurons). | Large gap between train/test performance suggests overfitting (high variance). |
| How does increasing the amount of training data generally affect bias and variance? | Increasing data primarily helps reduce variance. It doesn't significantly change bias (the model's inherent simplicity/complexity). More data helps the model generalize better from the noise. | More data fights high variance (overfitting). |
| Applying L2 regularization to a linear model increases its training error slightly but decreases its test error significantly. What happened? | The original model was likely overfitting. Regularization added a penalty, simplifying the model (reducing variance) at the cost of slightly increased bias (higher training error), leading to better generalization (lower test error). | Regularization trades a bit of bias for lower variance. |
(Note: This is a conceptual formula representing the expected prediction error)
Question 1: What is the fundamental difference between bias and variance in the context of machine learning models?
Bias refers to the error from incorrect assumptions in the learning algorithm (oversimplification), leading the model to miss relevant relations. Variance refers to the error from sensitivity to small fluctuations in the training set, causing the model to fit random noise rather than the intended output.
Question 2: How can you typically diagnose if your model is underfitting versus overfitting by looking at its performance on the training and test sets?
Underfitting (High Bias): The model performs poorly on BOTH the training set and the test set (high error / low accuracy on both).
Overfitting (High Variance): The model performs very well on the training set but poorly on the test set (low training error, high test error; large performance gap).
Question 3: Name two specific techniques primarily used to reduce overfitting in a neural network.
Two common techniques are:
1. Dropout: Randomly deactivating neurons during training.
2. Regularization (L1/L2): Adding a penalty for large weights to the loss function.
(Other valid answers include Early Stopping, Data Augmentation, reducing network size).
Question 4: Explain the general impact of increasing model complexity (e.g., using a higher-degree polynomial) on bias and variance.
Generally, increasing model complexity tends to decrease bias (as the model can fit more intricate patterns) but increase variance (as the model becomes more sensitive to the specific training data and noise).
Question 5: What is the significance of 'noise' or 'irreducible error' in the decomposition of a model's total error?
Noise represents the lower bound on the error that any model can achieve for a given dataset. It's due to inherent randomness or unmodeled factors in the data itself. While we aim to minimize bias and variance, we cannot reduce this irreducible error through modeling choices.
Launch your Graphy